completeness is overrated

Hannes Diener

University of Canterbury

Bishop style constructive mathematics.

“Mathematics with the use of intuitionistic logic (and some appropriate set-theoretic or type-theoretic foundations).”

Restricting the logic makes proving results harder and (sometimes impossible).

To “rescue results” we can either weaken the outcome, or strengthen the assumptions. There’s a few usual suspects.

P.S. Axiom of countable/dependent choice.

before I forget:

Joint work with Matthew Hendtlass.
Related work by Martin Escardó.

The following is a quote from “techniques of constructive analysis”.

In this chapter we discuss a peculiarly constructive technique that, normally under the hypothesis that one or more of the metric spaces under consideration is complete, enables us to prove results that otherwise would require some nonconstructive principle such as LPO, LLPO, or Markov’s principle.

The limited principle of omniscience LPO:
For any binary sequence $(a_n)_{n \geqslant 1}$ we have [ \fa{n \in \mathbb{N}}{a_n = 0} \ \lor \ \ex{n \in \mathbb{N}}{a_n=1} \ .] Or equivalently (modicum of choice) [\fa{x \in \mathbb{R}}{\left(x < 0 \ \lor x=0 \ \lor x>0\right)} \ .]
Weak LPO (WLPO) similar.

Example 1

Finding the square root of a complex number.

Example 2

Bishop’s Lemma

If $A$ is a complete, located subset of a metric space $(X,\rho)$, and $x \in X$, then there exists $y \in A$ such that if $x \neq y$, then $\rho(x,A)>0$.

(Bishop's Lemma is very useful for embedding functions $2^{\mathbb{N}} \to \mathbb{R}$ to $[0,1] \to \mathbb{R}$.)

Example 3

Ishihara’s first trick

Let $f$ be a strongly extensional mapping of a complete metric space $X$ into a metric space $Y$, and let $(x_{n})_{n \geqslant 1} $ be a sequence in $X$ converging to a limit $x$. Then for all positive numbers $\alpha \lt \beta$, either $\rho(f(x_{n}),f(x)) > \alpha$ for some $n$ or $\rho(f(x_{n}),f(x)) \lt \beta$ for all $n$.

Ishihara’s second trick

Let $f$ be a strongly extensional mapping of a complete metric space $X$ into a metric space $Y$, and let $(x_{n})_{n \geqslant 1}$ be a sequence in $X$ converging to a limit $x$. Then for all positive numbers $\alpha \lt \beta$, either $\rho(f(x_{n}),f(x)) \lt \beta$ eventually or $\rho(f(x_{n}),f(x)) > \alpha$ infinitely often.

Example 4

In constructive reverse mathematics

The following are equivalent:

$\mathrm{WMP}$ (Weak Markov’s Principle)
Every function on a c

(A function $f:X \to \mathbb{R}$ is strongly extensional, if, whenever $\vert f(x) - f(y)\vert \gt 0$, then $\rho(x,y) > 0$.)

Example 5

Assume $\lnot \mathrm{WLPO}$. If $X$ is complete then every function $f:X \to \mathbb{R}$ is non-discontinuous.

Example 6

If $X$ is complete then every sequentially continuous $f:X \to \mathbb{R}$ is strongly extensional.

Example 7: Putting it all together

The Kreisel-Lacome-Shoenfield Theorem (also Tseitin’s Theorem)

Assuming $\lnot \mathrm{WLPO}$, $\mathrm{WMP}$, and $\mathrm{BD}$-$\mathrm{N}$. Let $f:X \to \mathbb{R}$ be a mapping of a complete, separable metric space $X$. Then $f$ is point-wise continuous

Take $f:X \to \mathbb{R}$.

$\lnot\mathrm{WLPO}$ implies that $f$ is non-discontinuous. (requires $X$ complete)
$\mathrm{WMP}$ implies that $f$ is strongly extensional. (requires $X$ complete)
So together $f$ is sequentially continuous. (second trick, requires $X$ complete)
Finally $\mathrm{BD}$-$\mathrm{N}$ implies that $f$ is point-wise continuous. (requires $X$ separable)

In all of these examples we actually only ever needed the existence of a very special kind of Cauchy sequence.

Definition

Let $(X, \rho)$ be a metric space. For a sequence $x = (x_{n})_{n \geqslant 1}$ in $X$ converging to $x_{\infty} \in X$ and an increasing binary sequence $\lambda = (\lambda_{n})_{n \geqslant 1}$ we define a sequence $\lambda \circledast x $ by \begin{equation*} (\lambda \circledast x )_{n} = \begin{cases} x_{m} & \text{if } \lambda_{n} = 1 \text{ and } \lambda_{m}=1- \lambda_{m+1}, \\ x_{\infty} & \text{if } \lambda_{n} = 0. \end{cases} \end{equation*}

One can easily show that this is a Cauchy sequence.

Definition

A metric space $(X,\rho)$ is called complete enough, if for every sequence $x = (x_{n})_{n \geqslant 1}$ in $X$ converging to $x_{\infty} \in X$ and every increasing binary sequence $\lambda = (\lambda_{n})_{n \geqslant 1}$ the (Cauchy) sequence $\lambda \circledast x$ converges in $X$.

So if we can find an (interesting) space that is complete enough but not complete we have generalised (for free)

Ishihara’s tricks
Bishop’s Lemma (modulo details)
Kreisel-Lacome-Shoenfield Theorem. (Tseitin’s Theorem)
…

Rule of thumb: if it is classically true without completeness, but the constructive proof uses completeness, then it is constructively true assuming “complete enough”.

Some remarks.

Under the assumption of LPO every metric space is complete enough. (Actually this is an equivalence).
Every complete metric space is complete enough.
Not the best name (Matt’s suggestion is to call it substable).
Not the best notation.
Some variations in the definition possible.

The question remains:

Are there (constructively) any interesting examples of spaces that are complete enough, but not complete?

The original example of a complete enough space that is not complete was the space $\mathbf{P}$ of all permutations $\pi : \mathbb{N} \to \mathbb{N}$.

(This was useful in the following: The Riemann permutation theorem states that if every rearrangement of a series converges, then the series is absolutely convergent)

Are there any others?

Notice that $\mathbf{P}$ can be written in the form

[ \bigcap_{m \in \mathbb{N}} \bigcup_{n \in \mathbb{N}} \{f \in \mathbb{N}^\mathbb{N} \ \mid \ f(n)=m\} ] [ \qquad \cap \bigcap_{m \in \mathbb{N}} \{f \in \mathbb{N}^\mathbb{N} \ \mid \ \forall {i,j \leqslant m} : {f(i) \neq f(j)} \} \ ; ]

so $\mathbf{P}$ is a $G_\delta$ subset of Baire space.

In fact we can prove:

$G_\delta$ subsets of a complete enough space are also complete enough.

Actually:

Complete enough spaces are closed under arbitrary intersections.

This provides us with more examples for spaces that are complete enough, but not necessarily complete:

Open subsets of complete (enough) spaces,
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ is surjective} \}$,
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ attains $0$ infinitely often} \}$,
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ is increasing} \}$, (actually complete)
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ is strictly increasing} \}$, (actually complete)
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ is injective} \}$, (actually complete)

But there is more: the class of complete enough spaces is bigger than $G_\delta$

Every stable (a set $S$ is stable if $\neg \neg S \subset S$) subset of a metric space is complete enough.

So we have even more examples for spaces that are complete enough, but not necessarily complete:

The irrational numbers.
More general: any co-countable set.
Even more general: any set that is a complement.
$ \{f \subseteq \mathbb{N}^\mathbb{N} \ \mid \ f \text{ is not unbounded} \}$,

Matt’s view.

Let $\mathbb{N}_\infty$ be the space of all increasing binary sequences (with the metric induced by the one on Cantor space).

Write $\underline{n}$ for $0^n1111\dots$ and $\omega$ for $0000\dots$; that is

$\underline{0} = 1111111 \dots$
$\underline{1} = 0111111\dots$
$\underline{2} = 0011111\dots$
$\underline{3} = 0001111\dots$
$\vdots$
$\omega = 0000000\dots$

With classical logic we have $\mathbb{N}_\infty = \{\underline{n} : n \in \mathbb{N}\} \cup \{\omega\}$, but we cannot prove this constructively (to be precise this equality is equivalent to LPO).

Consider $\mathbb{N}$ as a subspace of $\mathbb{N}_\infty$. A space $X$ is complete, if every uniformly continuous function $f: \mathbb{N}\to X$ lifts to a uniformly continuous function $\bar{f}: \mathbb{N}_\infty \to X$.

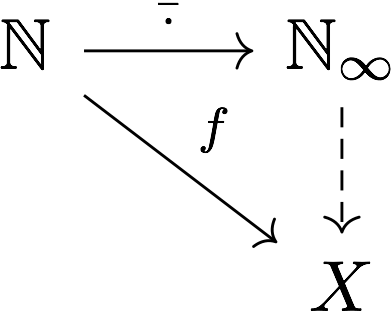
In contrast, a space $X$ is complete enough if every (uniformly) continuous function $f:\mathbb{N} \cup \lbrace \infty \rbrace \to X$ can be lifted to a (uniformly) continuous function $\bar{f}: \mathbb{N}_\infty \to X$.

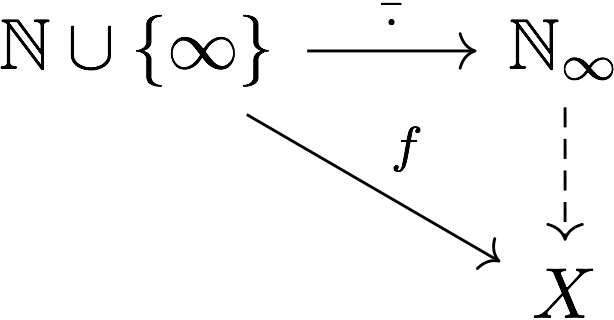
Closure properties

Closed under arbitrary intersections
Closed under cartesian product.
Not closed under unions.
Not preserved under (uniformly) continuous maps.

A different angle: impossible theorems

Consider the logical structure of Ishihara’s second trick: we have a constructively interesting $P$ and another alternative $Q$ such that [P \lor Q \ , ] where [Q \implies (\mathrm{W})\mathrm{LPO} \ .]

If we either assume $\mathrm{LEM}$ or $\lnot \mathrm{WLPO}$ then $P \lor Q$ is actually quite trivial. The surprising point is that we can prove $P \lor Q$ in BISH, that is without knowing whether we are in a classical or a constructive universe.

There are many similar results all based on the $\circledast$ construction.

My favourite impossible theorem.

Proposition

If [ \mathbb{R} = (-\infty,b \rbrack \cup (a, \infty) ] then either $a \lt b$ or $a = b$.

Furthermore in case the second alternative holds, $\mathrm{LPO}$ holds.

The proof doesn’t actually use the $\circledast$-construction:

Consider $z = b + (b-a) = 2b-a$…

The following generalisation, however, does involve complete enough.

Proposition

If $Q$ is a located subset of a complete enough metric space $(X, \rho)$ and $x \in X$ is such that [ \fa{z \in X}{z \neq x \ \lor z \notin Q} \ , ] then either $\rho(Q,x) \gt 0$ or $\rho(Q,x) = 0$.

Furthermore in case the second alternative holds, $\mathrm{LPO}$ holds.

Proposition

Let $f:\lbrack 0,1 \rbrack \to \mathbb{R} $ be such that $f(0)\cdot f(1) \leqslant 0 $ and let $\varepsilon \gt 0$. There exist $z \in \lbrack 0,1 \rbrack $ such that either $ \vert f(z) \vert \lt \varepsilon $ or there exists $ x_n \to z$ such that $f(z)\cdot f(x_n) \lt -\frac{\varepsilon}{8} $ for all $n$.

Furthermore, in case the second alternative holds, $\mathrm{WLPO}$ holds; and if $f$ is strongly extensional, then $\mathrm{LPO}$ holds.

Corollary

An increasing function $f :\lbrack 0,1 \rbrack \to \mathbb{R}$ has left and right limits.

Corollary

If $f :\lbrack 0,1 \rbrack \to \mathbb{R}$ is increasing then the points of discontinuity are enumerable.

Berger and Svindland have recently proved the following.

Proposition

Let $f :\lbrack 0,1 \rbrack \to \mathbb{R}^+$ be a quasi-convex, uniformly continuous function. Then either the infimum of $f$ is positive.

We can turn this into an impossible theorem.

Proposition

Let $f :\lbrack 0,1 \rbrack \to \mathbb{R}^+$ be a quasi-convex function such that $\inf\set{f(x)}{x\in I}$ exists for each sub-interval $I$ of $\lbrack 0,1 \rbrack$. Then either the infimum of $f$ on $\lbrack 0,1 \rbrack$ is positive or $\inf f = 0 $.

Furthermore in case the second alternative holds $\mathrm{WLPO}$ holds.

Thoughts:

Is any of this known?
complete-enoughication of the rationals?
compact enough?