Philipp Wacker 
Senior Lecturer in Statistics
Department of Mathematics and Statistics
University of Canterbury
Private Bag 4800
Christchurch, NEW ZEALAND
philipp.wacker@canterbury.ac.nz
Graduate Student Supervision
I welcome inquiries regarding graduate student supervision, summer projects, and other ways of getting involved in doing mathematical and statistical research. Please write me an email if you are interested in chatting about possible projects! See below for a snapshot of things I am working on. I am interested in both pure (fundamental mathematical/statistical) research as well as applied projects with computational aspects (usually done in Python or R).
Research Interests and Current Projects
I am a mathematician and statistician with research expertise in the analysis and development of particle-based algorithms for optimization, sampling, and inference. I am usually working on various aspects of Bayesian inversion in the broader sense, with a focus on mathematical analysis and efficient implementation.
I am currently involved in research programmes on:
Filtering, Parameter Inference, Inverse Problems
 Many computational problems in engineering, biology, geology, numerical weather forecasting, medical imaging, etc. can be formulated as an inverse problem:
Many computational problems in engineering, biology, geology, numerical weather forecasting, medical imaging, etc. can be formulated as an inverse problem:
- We are often interested in a hidden parameter. This can be a physical constant, an exponential growth rate, the hydraulic conductivity of the subsurface as a scalar field, the air pressure and temperature at every point in the atmosphere, the location of a certain malignous growth in a patient's body, etc.
- Usually this hidden parameter is a priori difficult to access: We cannot directly observe the exponential growth rate of a cryptic bird species which is hard to observe, we don't have enough measurement balloons to map every point of the atmosphere, and we do not want to cut open a patient unnecessarily.
- This means we have to resort to indirect methods of getting information about this parameter, e.g. by observing a different, more easily measured species in the same ecosystem; by combining different data sources, like satellites, ground stations, buoys; or by doing X-ray tomography.
- This means we now have to use this indirect measurement, which is often incomplete and noisy (i.e. perturbed by, e.g., measurement noise), to extract information about our original quantity of interest.
 The Analysis of the Ensemble Kalman filter, and its application to optimization and sampling
The Analysis of the Ensemble Kalman filter, and its application to optimization and sampling
The Ensemble Kalman approach is a highly successful method used in numerical weather forecasting and geophysical applications. The idea is to sprinkle the parameter space with particles (forming the ensemble) and moving this collective of particles in parameter space towards more suitable regions. In filtering and sampling problems these particles would ideally be moved such that they approximate the posterior measure after incorporating data, and in optimization/inversion we would try to move them towards minima of the data discrepancy functional.
 Nested Sampling and its application to rare event estimation
Nested Sampling and its application to rare event estimation
Nested Sampling is a sampling and quadrature method employed for settings where the integrand (or the likelihood function) is extremely narrow, or is concentrated in a region of almost vanishing prior mass. This arises for example in high-dimensional inference problems, and for rare event estimation. Nested Sampling manages an ensemble of "live points" which climb up level sets of the integrand, using a clever statistical trick to approximate the prior mass contraction in the process. There is ongoing research both about the methodology in general (i.e. its well-posedness, its analytical properties, and convergence behavior) as well as concrete applications of this technique.
 Derivative-free optimization, in particular Consensus-based Optimization
Derivative-free optimization, in particular Consensus-based Optimization
Consensus-based optimization is a relatively recent derivative-free (zero-order) optimization method. In contrast to methods like gradient descent or quasi-Newton-type methods we assume that we cannot evaluate gradient information of the minimzation functional. Consensus-based optimization tracks an ensemble of particles weighted by their pointwise evaluations in this functional, coupled with a contraction towards their weighted mean, and an explorative diffusion.
Maximum-a-posteriori estimators and their well-posedness in infinite-dimensional Bayesian inverse problems
The MAP estimator is an object that couples together 'classical' inversion (via regularization techniques like Tikhonov-Phillips) and Bayesian inversion. In infinite dimensions there are many different ways of defining a 'maximum' of the posterior, which is not easily done since there is not Lebesgue measure and thus no probability density in infinite dimensions. Connecting these different notions (strong modes, weak modes, global weak modes, universal modes, generalized modes, ...) is an interesting research topic that touches stochastic analysis, functional analysis, reproducing kernel Hilbert spaces, and others.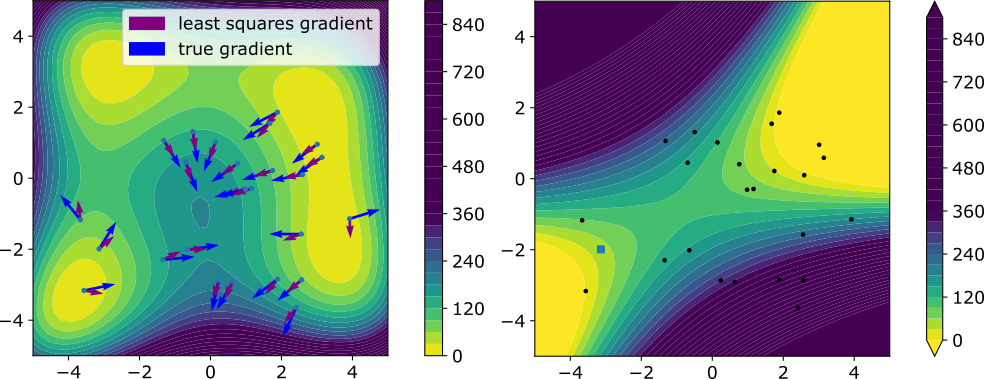 Statistical Linearization, localization, and other tricks for approximate gradient inference
Statistical Linearization, localization, and other tricks for approximate gradient inference
In some settings it is very computationally expensive (or impossible) to acquire gradient information about a potential (e.g. one used in a sampling or optimization task). Methods like the Ensemble Kalman method circumvent this problem by implicit statistical linearization, which yields indirect gradient information. Unfortunately, this approach is limited to settings where the problem is 'sufficiently' linear. I am interested in alternative methods of turning pointwise evaluation into differential information.
I am happy to provide research support and collaboration. Please contact me by email.
