Current Research Projects
-
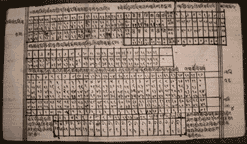 Numerical Tables and associated computational algorithms in Sanskrit sources
Numerical Tables and associated computational algorithms in Sanskrit sources
Numerical tables, a significant yet often overlooked source in the history of mathematics, not only hold intrinsic mathematical interest with respect to the computational techniques they embody, but also more broadly as they speak to scientific practices, assumptions, and aspirations of those that compiled them. However the significance of mathematical tables and computational techniques often goes unnoticed, due largely to their subordinate role in classical and modern mathematics. Neglect of these subjects in the history of mathematics has led to a widespread failure to understand the role of computational practices in shaping scientific ideas. This research project undertakes to remedy this situation by an in-depth investigation of tables and computation algorithms in the mathematics of India in the second millennium, documenting and analyzing the growing importance and eventual dominance of computational mathematics in the Sanskrit exact sciences.
-
 The History of Mathematical Astronomy in the Indian subcontinent
The History of Mathematical Astronomy in the Indian subcontinent
The astral sciences in the Indian subcontinent---that is, mathematics, astronomy, and related disciplines---have been flourishing for over two and a half millennia, and this culture of inquiry has produced insights and techniques that are central to many of our scientific practices today, such as the base ten decimal place value system and trigonometry. Indeed, many of their technical procedures, such as infinite series expansions for various mathematical relations predated those that were developed with the advent of the Calculus, but notably in contrasting intellectual circumstances with distinctly different epistemic priorities. However, while many histories of science have centered on the so-called `western miracle' in their analysis of the ignition and flourishing of modern science, they have done so at the expense of other non-European traditions. Yet these traditions can provide some powerful contrasts and cross-cultural comparisons for our attempts to delineate and illuminate the scope of scientific activity more broadly. This comprehensive and far reaching research programme aims to rectify this disparity by bringing more prominently into the mainstream key perspectives, features, and themes of this important, yet understudied, tradition of scientific inquiry.
-
 Āmarāja's (ca. 12th century) commentary on Brahmagupta's Khaṇḍakhādyaka
Āmarāja's (ca. 12th century) commentary on Brahmagupta's Khaṇḍakhādyaka
The critical edition and commentary of a seventh century Sanskrit work in mathematical astronomy: the Commentary on Brahmagupta's Khaṇḍakhādyaka by Āmarāja, a twelfth century commentator. This work was written according to the so-called Midnight school and covers topics such as planetary positions and motions, eclipses, trigonometry, time-keeping, rising and setting of planets, the moon's cusps and stars.
-
 Greek and Arabic diagrammatic reasoning
Greek and Arabic diagrammatic reasoning
The investigation of Greek texts and manuscripts on mathematics and astronomy, with particular emphasis on the role and nature of their technical diagrams. Diagrams represent an element of mathematical reasoning which is not part of the written text. Are they complementary or independent of the text?
-
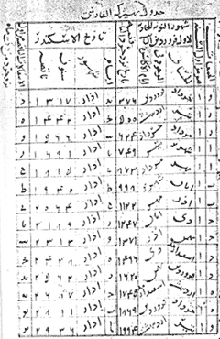 The Zīj al-Sanjarī
The Zīj al-Sanjarī
The critical edition and commentary of the twelfth century Arabic work in mathematical astronomy, the Zīj al-Sanjarī by Al-Khāzinī. Zīj is a term derived from middle-Persian that was used to refer to compositions containing astronomical tables and accompanying descriptions intended for practical astronomical use. They typically include chronological systems and calendar conversions, mean motions and corresponding planetary equations, trigonometric functions, stellar coordinates, eclipses, and so on.
-
 The role and function of mathematical notation and symbolism. What are some of the various notational conventions in mathematics and why and how did they develop? What do they reveal about the mathematical object in question? How does notation play an important role in facilitating mathematical insights? These question are
particularly interesting when considering the emergence of symbols for various aspects of calculus in the seventeenth century and beyond.
The role and function of mathematical notation and symbolism. What are some of the various notational conventions in mathematics and why and how did they develop? What do they reveal about the mathematical object in question? How does notation play an important role in facilitating mathematical insights? These question are
particularly interesting when considering the emergence of symbols for various aspects of calculus in the seventeenth century and beyond.
